[bn]Procedural Content Generation 1: Noise

2022-11-21

---

---

"Knowing yourself is the beginning of all wisdom"
-Aristotle

 

 

ছবির তিনটা মিনিয়নকে মনে আছে? Kevin, Stuart আর Bob। Despicable Me এর ডিরেক্টরের কথা অনুসারে, Gru এর মিনিয়নের সংখ্যা ১০৪০০। এবার একটু খেয়াল করে দেখো, প্রত্যেকটা মিনিয়ন কি দেখতে হুবহু Kevin, Stuart আর Bob এর মতই?

না। ১০৪০০ মিনিয়নের সবাই এই তিনজনের ক্লোন না। তাহলে প্রতিবার যখন ওরা স্ক্রিনে আসতো, একই চেহারা দেখতে দেখতে তুমি বোর হয়ে যেতে। কিন্তু মুভির 3D মডেলিং আর্টিস্টরা নিশ্চয়ই বসে বসে ১০৪০০টা মডেল বানায় নাই। ব্যাপারটা একদিকে যেমন একঘেয়ে আর সময়সাপেক্ষ, তেমনি এক ধরনের দশ হাজার মডেল বানানোটা অবশ্যই মুভির বাজেটকে সাপোর্ট করবে না। একটা এনিমেটেড মুভি বানাতে আরো হাজারটা কাজের দিকে খেয়াল রাখতে হয়। তাহলে উপায় কী?

কোলাজের ৯টা ভিডিও গেমই বেশ জনপ্রিয়। বাম থেকে ডানে (এরপর উপর থেকে নিচে) ক্রমানুসারেঃ

• No Man's Sky
• Spelunky
• Factorio
• Minecraft
• Terraria
• RimWorld
• Valheim
• Civilization
• Dwarf Fortress

এদের মধ্যে Minecraft বোধকরি সবথেকে জনপ্রিয়। একটা মজার ব্যাপার হল, আমি প্রথমবার Minecraft অন করলে যেই ম্যাপে খেলব, অন্য কেউ তার কম্পিউটারে একই ম্যাপ পাবে না। তুমি New Game এ ক্লিক করলে গেম তোমার জন্য একটা ম্যাপ জেনারেট করে দেয় আর এই ম্যাপ সবার জন্য আলাদা। এদের মধ্যে সাদৃশ্য থাকবে, কিন্তু হুবহু এক হবে না। এই Generated Environment এর একটা বড় সুবিধা হচ্ছে, মানুষভেদে গেমপ্লে এক্সপেরিয়েন্স আলাদা আলাদা হয়। আমি খেলার সময় যে এনভায়রনমেন্ট বা সিচুয়েশন পাচ্ছি, অন্য কেউ তার চেয়ে আলাদা আর unique একটা এক্সপেরিয়েন্স পাবে। ম্যাপ জেনারেট করার আরেকটা কারণ হচ্ছে, Minecraft এর ওয়ার্ল্ড অসীম (infinite)। তুমি যদি কোনো একটা দিক ধরে অনন্তকালও হাঁটতে থাকো, তবুও এর শেষে পৌঁছাতে পারবে না। কিন্তু কোনো গেম ডেভেলপারের পক্ষে অসীম সংখ্যক মডেল, রিসোর্স, কনটেন্ট বানানো সম্ভব না অবশ্যই। তাই প্রোগ্রামাররা এমন প্রোগ্রাম লেখে যেন সেটা গেমের দরকার মত নতুন নতুন কনটেন্ট জেনারেট করতে পারে। এই প্রসেসকে আমি বলছি Content Generation.

লিস্টের প্রতিটা গেমই কোনো না কোনো ভাবে Computer Generated Content ব্যবহার করে। No Man's Sky এর ১৮ কুইন্টিলিয়ন গ্রহের প্রায় প্রতিটি Computer Generated. ১ কুইন্টিলিয়ন মানে হচ্ছে ১ এর পর ১৮টা শুন্য। Spelunky'র লেভেলগুলো প্রতিবার আলাদাভাবে সাজানো থাকে। Factorio'র এলিয়েন গ্রহের মাটি, পানি, গাছ, মিনারেল সবকিছুই কম্পিউটারের ক্যালকুলেশন অনুযায়ী জেনারেট হয় - আর অবশ্যই প্রতিবার আলাদাভাবে।

ধরো, আমরা Minecraft এর মত একটা 2D ম্যাপ জেনারেট করতে চাই, যেখানে র‍্যান্ডমলি মাটি, পানি, ঘাস, গাছ ছড়ানো ছিটানো থাকবে। অনেকটা উপরের ছবির মত । এখানে হালকা সবুজ (L), মাঝারি সবুজ (G), গাঢ় সবুজ (D) আর নীল (B) রঙের অংশগুলোকে আমি যথাক্রমে ছোট ঘাস, বড় ঘাস, ঘন গাছপালা আর নদী ধরছি।

এরকম একটা ম্যাপ তৈরির জন্য একজন বিগিনারের মাথায় সবার আগে যে মেথড আসে সেটা হলো, আমরা একটা একটা করে পয়েন্ট ধরব আর র‍্যান্ডমলি এদেরকে L/G/D/B কালার দিতে থাকব। এইভাবে সবগুলো পয়েন্টের উপর একটা লুপ চালালে নিচের মতো আউটপুট পাবো।

from matplotlib import pyplot as plt
import numpy as np
import random

# প্রত্যেকটা রঙের RGB value
colors = [
    (66, 135, 245), # blue
    (0, 235, 105), # light green
    (0, 189, 85), # green
    (14, 99, 52), # dark green
]

# আমাদের environment এর সাইজ (দৈর্ঘ্য আর প্রস্থ)
SIZE = 16

# নতুন একটা SIZE x SIZE পিক্সেলের environment বানাই
world = np.zeros((512, 512, 3))

for a in range(SIZE):
    for b in range(SIZE):
        world[a][b] = random.randint(0, len(colors)-1)

plt.imshow(world)
plt.show()

দেখে কি মনে হচ্ছে? হিজিবিজি, তাই না?

এবার একটু বড় স্কেলে দেখি।

আরো হিজিবিজি।

আমরা একটা পরিবর্তন আনতে পারি। একটা এনভায়রনমেন্টে সবধরনের জিনিস থাকার সম্ভাবনা একই না। ধরি, L, G, D, B এর সম্ভাবনা যথাক্রমে ৫০%, ২৫%, ১৫% আর ১০%। মানে সবথেকে বেশি পরিমাণে থাকবে হালকা ঘাস, তার অর্ধেক থাকবে বড় ঘাস, তারও প্রায় অর্ধেক বন-জঙ্গল, আর পুরো ম্যাপের মাত্র দশ ভাগের এক ভাগ থাকবে নদী।

L = (0, 235, 105) # light green
B = (66, 135, 245) # blue
G = (0, 189, 85) # green
D = (14, 99, 52) # dark green


SIZE = 64

world = np.zeros((SIZE, SIZE, 3), np.uint8)

for a in range(SIZE):
    for b in range(SIZE):
        random_number = random.randint(0,100)
        if 0 <= random_number <= 50:
            world[a][b] = L
        elif 50 <= random_number <= 75:
            world[a][b] = G
        elif 75 <= random_number <= 90:
            world[a][b] = D
        elif 90 <= random_number <= 100:
            world[a][b] = B

আগের থেকে একটু ভালো হয়ত, তবে কাজ চালানোর মত না। একটু চিন্তা করো, এখানে সমস্যাটা কোন জায়গায়?

আমরা র‍্যান্ডমলি প্রতিটা পিক্সেলে কালার এসাইন করছি। কিন্তু তুমি যখন Minecraft খেল, নিশ্চয়ই তোমার সামনে র‍্যান্ডমলি ঘাস আর পানির ব্লক ছড়ানো-ছিটানো থাকে না। একটা ঘাস ব্লকের আশেপাশে আরো বেশ কিছু ঘাস ব্লক থাকবে। হঠাৎ করে একটা-দুইটা পানির ব্লক জেনারেট হয়ে জেনারেশন বন্ধ হয়ে যাবে না। মানে একই ধরনের অনেকগুলো ব্লক একত্রে থাকবে (Fig-1 এর মত)।

 

 

Random Generation VS Procedural Generation

Despicable Me ফ্র্যাঞ্চাইজির মিনিয়নগুলোর কিছু ফিচার এরকমঃ

• মিনিয়নের আকার তিন রকম। বেঁটে আর গোলগাল, মাঝারি, লম্বা আর ছিমছিমে।
• মিনিয়নের চোখ থাকবে ১টা বা ২টা।
• মিনিয়নের হেয়ারস্টাইল ৫ ধরনের। Bald, Buzz Cut, Sprouted, Spiky আর Combed.
• লম্বা মিনিয়নের হেয়ারস্টাইল সাধারণত Sprouted
• ১ চোখওয়ালা মিনিয়নগুলো সাধারণত বেঁটে হয়

মানে আমি চাইলেই একটা মিনিয়ন জেনারেট করতে পারব না যার ফিচারসেট হচ্ছে [ লম্বা, একচোখ, Bald ]। Random Generation হচ্ছে তুমি ইচ্ছামত কোনো নিয়ম না মেনে কন্টেন্ট জেনারেট করবা, যেমনটা আমরা করছিলাম কিছুক্ষণ আগে। আর Procedural Generation হচ্ছে কোনো একটা Procedure (শর্ত বা নিয়মকানুন) মেনে কন্টেন্ট জেনারেট করা। সেটা হতে পারে মিনিয়নের এই ফিচার গুলো মানার procedure, অথবা "একটা ম্যাপে একই ধরনের বেশকিছু পিক্সেল একত্রে থাকবে" - এটা মানার procedure।

 

ম্যাপ জেনারেশনে ফেরত আসি। একই কালারের পিক্সেল গুলো পাশাপাশি থাকার জন্য আমাদের এমন এলগরিদম দরকার যাতে একটা কালার হুট করে আরেকটা কালারে চেঞ্জ না হয়। মানে আমাদের Reality VS Expectation অনেকটা এরকম।

আলোচনার সুবিধার্থে আমরা আপাতত কালার নিয়ে মাথা ঘামাচ্ছি না। Fig-6 হচ্ছে আমাদের Expectation। লক্ষ্য করে দেখ, প্রতিটা পিক্সেলের কালারের সাথে তার আশেপাশের পিক্সেলের কালারের সাদৃশ্য রয়েছে। কালারগুলো gradually পরিবর্তন হচ্ছে। ছবিটা আরেকটু জুম-ইন করলে দেখতে এমন লাগবে।

যারা ইমেজ এডিটিং বা ইলাস্ট্রেশনের কাজ করে, তাদের কাছে এই ছবিটা অনেক পরিচিত। ফটোশপে গ্রেডিয়েন্ট টুল নিয়ে ক্যানভাসে টান দিলে এই রকম কালার গ্রেডিয়েন্ট পাওয়া যায়। কম্পিউটার সায়েন্সের ভাষায় গ্রেডিয়েন্ট নয়েজ (Gradient Noise)। আর আমরা এতক্ষন র‍্যান্ডমলি পিক্সেলগুলো তে কালার ভ্যালু বসিয়ে যা পাচ্ছিলাম, সেটা হচ্ছে White Noise।

 

 

Noise কী?

সাধারণত আমরা ফোনে কথা বলার সময় বলি, "পেছন থেকে নয়েজ আসছে"। অথবা একটা ছবি তোলার পর ভালো না আসলে বলি ছবিতে নয়েজ আছে। সাধারণ অর্থে নয়েজ হচ্ছে অপ্রয়োজনীয় অংশ। কিন্তু আরেকভাবে বলা যায়, নয়েজ হচ্ছে Random entity। আমরা আমাদের প্রয়োজনে নয়েজের এই ডেফিনিশন নিয়ে আগাবো। আমাদের সুবিধার্থে, Noise হচ্ছে কিছু র‍্যান্ডম সংখ্যা। Content Generation এ আমাদের লক্ষ্য হচ্ছে নয়েজ দিয়ে ভ্যারিয়েশন তৈরি করা। Random generation এ আমরা এই সংখ্যা গুলো বাছাই করি কোনো ধরনের কন্টেক্সট (Context) ছাড়া। অর্থাৎ যেকোনো একটা সংখ্যা বাছাইয়ের জন্য আমরা এর আশেপাশের এনভায়রনমেন্টের দিকে গুরুত্ব দেই না। অন্যদিকে, Procedural Generation এর জন্য আমাদেরকে এদিকে গুরুত্ব দিতে হয়, অর্থাৎ আমরা কোনো একটা নির্দিষ্ট ফিচারওয়ালা নয়েজ চাই। যেমনঃ পর্বতের আশেপাশে ছোট ছোট টিলা থাকবে, এইটা একটা ফিচার।

এখন, আমরা কিভাবে নয়েজ জেনারেট করতে পারি? র‍্যান্ডম নয়েজ আমরা কোড করলাম একটু আগে। আরেকটা উপায় হতে পারে সাইন/কোসাইন ফাংশন ব্যবহার করা, কারণ এসব ফাংশনের পরপর আউটপুট ভ্যালুগুলো ধীরে ধীরে পরিবর্তন হয়। কিন্তু এধরনের ফাংশনের সমস্যা হচ্ছে যে, কিছু সময় পর নয়েজ রিপিট হওয়া শুরু করবে। কারন সাইন/কোসাইন ফাংশনের পিরিয়ড হচ্ছে ৩৬০ ডিগ্রী। অর্থাৎ ৩৬০ ডিগ্রী পর পর ফাংশনটা একই ভ্যালু দিবে। আমরা যদি True variation চাই, তাহলে এই ফাংশনেও আমাদের কাজ হবে না।

আমাদের মূল আলোচনা গ্রেডিয়েন্ট নয়েজ নিয়ে। এর সুবিধা হচ্ছে যে, নয়েজ আউটপুট ধীরে ধীরে পরিবর্তন হওয়া সত্ত্বেও কিছুক্ষণ পর পর নয়েজ ভ্যালু রিপিট হতে থাকবে না। গ্রেডিয়েন্ট নয়েজের সর্বপ্রথম ইমপ্লেমেন্টেশন করেন Ken Perlin, ১৯৮৫ সালে, Perlin Noise নামে। ২০০১ সালে তিনিই Simplex Noise নামে আরেক ধরনের নয়েজ পেটেন্ট করেন। Simplex আর Perlin নয়েজ অনেকটা একরকম হলেও, Simplex Noise এর টাইম কমপ্লেক্সিটি আগের চেয়ে ভালো আর আরো বেশি ডাইমেনশন এর নয়েজ জেনারেট করতে পারে। Simplex এর ওপেনসোর্স ইমপ্লেমেন্টেশন হচ্ছে OpenSimplex। তবে আমরা শুধু Classic Perlin Noise নিয়ে আলোচনা করব। কারণ Perlin Noise এর মূলতত্ত্ব প্রায় সবজায়গায় ব্যবহারযোগ্য।

 

 

Dot Products

আমরা জানি, দুইটা ভেক্টরের ডট প্রোডাক্ট,

\(\hat{a}\cdot\hat{b} = \mathbf{ab}\cos\theta\)। ধরি, \(\hat{a}\) আর \(\theta\) ধ্রুবক। তাহলে,

\(\hat{a}\cdot\hat{b}\propto b\)

মানে আমাদের ভেক্টর দুইটার একটাকে যদি স্থির রাখি (\(\hat{a}\)), আর তাদের মধ্যের কোণ যদি পরিবর্তন না করি, তাহলে তাদের ডট প্রোডাক্ট অন্য ভেক্টরটার (\(\hat{b}\)) দৈর্ঘ্যের সাথে বাড়বে/কমবে। তাহলে \(\hat{b}\) এর হেড আর \(\hat{a}\) এর টেইল সবসময় একই পয়েন্টে রেখে যদি নিচের মতো করি,

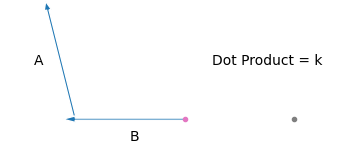
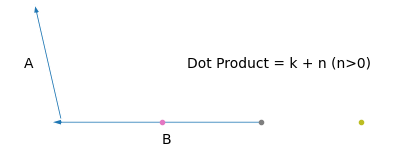
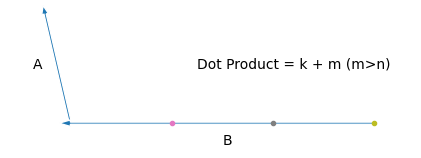
দেখো, \(\hat{b}\) এর টেইল আমরা যত ডানে সরাচ্ছি, এর ডট প্রোডাক্টের মানও বাড়ছে। \(hat{b}\) এর \(y\) অক্ষ বরাবর অবস্থান ধ্রুব রেখে \(x\) অক্ষে \([0,39]\) রেঞ্জে ডট প্রোডাক্টের মান আসে অনেকটা এরকম।

[[  0.  -2.  -4.  -6.  -8. -10. -12. -14. -16. -18. -20. -22. -24. -26.
  -28. -30. -32. -34. -36. -38. -40. -42. -44. -46. -48. -50. -52. -54.
  -56. -58. -60. -62. -64. -66. -68. -70. -72. -74. -76. -78.]]

ভ্যালুগুলোকে Grayscale Image এর কালার ভ্যালুর রেঞ্জে আনলে (255- Brightest, 0-Darkest),

[[255.         248.46153846 241.92307692 235.38461538 228.84615385
  222.30769231 215.76923077 209.23076923 202.69230769 196.15384615
  189.61538462 183.07692308 176.53846154 170.         163.46153846
  156.92307692 150.38461538 143.84615385 137.30769231 130.76923077
  124.23076923 117.69230769 111.15384615 104.61538462  98.07692308
   91.53846154  85.          78.46153846  71.92307692  65.38461538
   58.84615385  52.30769231  45.76923077  39.23076923  32.69230769
   26.15384615  19.61538462  13.07692308   6.53846154   0.        ]]

যদি \(\hat{b}\) এর টেইল কোনো পিক্সেলের পজিশন হয়, আর ডট প্রোডাক্টের মান brightness হয়, তাহলে যথেষ্ট পরিমাণ পজিশনের জন্য আমরা একটা গ্রেডিয়েন্ট পাব।

এখন একটা জিনিস খেয়াল করো, আমাদের গ্রেডিয়েন্ট সবসময় 0 থেকে 255 অথবা 255 থেকে 0 তে যাচ্ছে (তোমার ফিক্সড ভেক্টরকে বিভিন্নভাবে ঘুরিয়ে দেখো)। এর কারণ আমাদের গ্রেডিয়েন্ট স্কেলের বামে এখন ফিক্সড ভেক্টরটা আছে। আমরা যদি ডানে ভেক্টরওয়ালা একটা গ্রেডিয়েন্ট স্কেল নিই,

আর এই দুইটাকে overlap করি,

এখন ভেক্টর দুইটাকে বিভিন্নভাবে পরিবর্তন করে দেখো কেমন আউটপুট পাও।

 

---

 

আমাদের সিস্টেমটা এখন পর্যন্ত এরকম,

আমরা প্রতিটা পয়েন্টের জন্য বামের ভেক্টরের সাথে ডট আর ডানের ভেক্টরের সাথে ডট করছি, এরপর দুইটা ডটের মাঝামাঝি কোনো একটা ভ্যালু নিচ্ছি (যেটাকে কিছুক্ষণ আগে overlap বললাম)। এখন এই মাঝামাঝি ভ্যালু পাবো কোথায়?

 

 

Linear Interpolation (Lerp)

ধর আমাদের কাছে দুইটা data point \(a\) আর \(b\) আছে। এরা বিন্দু, ভেক্টর যা ইচ্ছা হতে পারে যতক্ষণ পর্যন্ত এই ডেটা পয়েন্ট দিয়ে আমরা বিয়োগ আর স্কেলার গুণন করতে পারব। আমরা এই দুইয়ের মধ্যবর্তী ডেটা পয়েন্ট চাইলে কি করি? এর গড় নিই।

\(P(x,y) = \frac{A(x_0,y_0) + B(x_1, t_1)}{2}\); যদি \(A\) আর \(B\) দুইটা বিন্দু হয়।

\(\Rightarrow P(x,y) = 0.5A + 0.5B\)

একে আরেকভাবে দেখলে বলা যায়, \(P\) এর সাথে \(A\) এর সাদৃশ্য ৫০% আর \(B\) এর সাদৃশ্য ৫০%। অথবা, \(A\) থেকে \(B\) এর মধ্যের রাস্তার ৫০% দূরত্বে \(P\) আছে (Fig-13)। অথবা, যদি আমরা A ডেটা পয়েন্টকে B তে transform করতে চাই, তাহলে আমরা আমাদের transformation process এর ৫০% সম্পন্ন করেছি (Fig-14)। যখন আমরা ০% এ আছি, তার মানে আমাদের সম্পূর্ণ বৈশিষ্ট্য \(A\) এর মত, আর যখন আমরা ১০০% এ আছি তখন পুরোপুরি \(B\) এর মত। যারা আরেকটু ঘাঁটাঘাঁটি করে অভ্যস্ত, তারা হয়ত বুঝে গেছ যে, Lerp আর Weighted Average একই জিনিস।

তাহলে যদি আমরা এমন একটা ভেক্টর চাই যেটা দুইটা ভেক্টর \(A\) আর \(B\) এর মধ্যে পরেরটার সাথে ৭০% সাদৃশ্যপূর্ণ, তাহলে-

\(V = 0.3A + 0.7B\)

আর যদি \(t\) পরিমাণ সাদৃশ্য থাকে,

\(V = (1-t)A + tB;\ \ \ 0\le t \le 1\)

ধরি, আমাদের কাছে দুইটা পিক্সেলের ব্রাইটনেস ভ্যালু আছে। A - 121 আর B - 245। আমরা চাই, আমাদের রেজাল্ট পিক্সেলের ব্রাইটনেস ভ্যালুর ৮০% B এর ব্রাইটনেস ভ্যালুর মত হবে আর বাকিটা A এর মত হবে।

\(P = 0.2 \times 121 + 0.8 \times 245 = 196\)

উপরের overlap প্রসেসের জন্য আমরা Lerp ব্যবহার করেছি। কিন্তু এখানে \(t\) এর ভ্যালু কি হবে? আমরা ভেক্টর দুইটার মাঝখানে যতটুকু দূরত্বে আছি (বাম পাশের ভেক্টর থেকে) সেটাই। তাহলে প্রতিটা পিক্সেলের জন্য \(t = [0, \frac{1}{39}, \frac{2}{39}, \frac{3}{39}, ..., 1]\), এখানে 0 মানে সম্পূর্ণ A এর মত আর 1 মানে সম্পূর্ণ B এর মত।

Note: ম্যাথম্যাটিকসে Lerp অনেক কাজের একটা ফাংশন। আমরা যেমন উপরের ছবিতে একটা ভেক্টরকে আরেকটা ভেক্টরে ট্রান্সফর্ম করলাম তেমনি যেকোনো টাইপের ডেটাকে আমরা এই ফাংশনে ব্যবহার করতে পারব যতক্ষণ আমরা বিয়োগ আর স্কেলার গুণণ করতে পারছি। গেম ডেভেলপমেন্টে প্রায় সবধরনের কাজে Lerp দরকার হয়।

 

---

 

আমরা দুইটা ভেক্টরের একটা সেগমেন্টের বদলে আরো বেশি ভেক্টরের যত খুশি সেগমেন্ট নিয়ে আরো বড় দৈর্ঘ্যের গ্রেডিয়েন্ট স্কেল বানাতে পারি। প্রতিবার কোনো পিক্সেলের Grayscale ভ্যালু সেট করার সময় এর সেগমেন্টের বামপাশের আর ডানপাশের ভেক্টর এর সাথে ডট প্রোডাক্ট নিয়ে Lerp করব। আর দুইটা সেগমেন্টের মাঝে একটা সাধারণ ভেক্টর থাকার কারণে এদের মধ্যে ট্রানজিশনও গ্রেডিয়েন্ট হবে। কারণ প্রথম সেগমেন্টের শেষ ভ্যালু \((t=1 \rightarrow (1-1)\times A + 1\times B = B)\) আর দ্বিতীয় সেগমেন্টের শুরুর ভ্যালু \((t=0 \rightarrow (1-0) \times B + 0 \times C = B)\) একই। আর এই জিনিসকে যদি \(y\) অক্ষের দিকেও বর্ধিত করি, তাহলে-

কোনো পিক্সেলের জন্য চারটা ভেক্টরের সাথে ডট প্রোডাক্টগুলো \(d_0, d_1, d_2, d_3\) (Topleft থেকে clockwise) হলে, ফাইনাল ভ্যালু-

\(d = F(F(d_0, d_1, x), F(d_2, d_3, x), y)\)

যেখানে,

\(\text{Lerp of two Numbers}, F(a, b, t) = (1-t)A + tB\)

\(x,y\) হচ্ছে সেগমেন্টে \(x\) আর \(y\) coordinate এর রিলেটিভ পজিশন। আর আমরা যে ভেক্টরগুলো কে ফিক্সড রাখছি, সেগুলো হচ্ছে ইনফ্লুয়েন্স ভেক্টর (Influence Vector)।

আমরা আমাদের থিওরির বেশিরভাগ জিনিস আলোচনা করে ফেলেছি। কোথাও এখনো ঝাপসা লাগলে আরেকবার পড়ে বোঝার চেষ্টা করো।

এবার আমরা কোড করা শুরু করব।

from matplotlib import pyplot as plt
import random
import math
import numpy as np

SIZE = 32 # আমাদের ইমেজের দৈর্ঘ্য আর প্রস্থ (পিক্সেলে)
S = 8 # প্রতিটা সেগমেন্টে কতটা পিক্সেল চাই

influence_vectors = {} # আমাদের ইনফ্লুয়েন্স ভেক্টরগুলো রাখার জন্য ডিকশনারি

এরপর আমরা ক্যালকুলেট করব কোন কোন পজিশনে আমাদের ইনফ্লুয়েন্স ভেক্টরগুলা থাকবে।

for i in range(0, SIZE+1, S):
    for j in range(0, SIZE+1, S):
        influence_vectors[(i,j)] = {}
	influence_vectors[(i,j)]["angle"] = random.randint(0,360)

আমাদের ডিকশনারিতে Key হবে ভেক্টরের পজিশন আর Value হবে ভেক্টরের Properties (এক্ষেত্রে x অক্ষের সাপেক্ষে ভেক্টরের কোণ)। হিসাবের সুবিধার জন্য আর ডট প্রোডাক্টগুলোর অনুপাত ঠিক রাখার জন্য আমরা সবগুলো ভেক্টরকে একক ভেক্টর হিসেবে ধরছি।

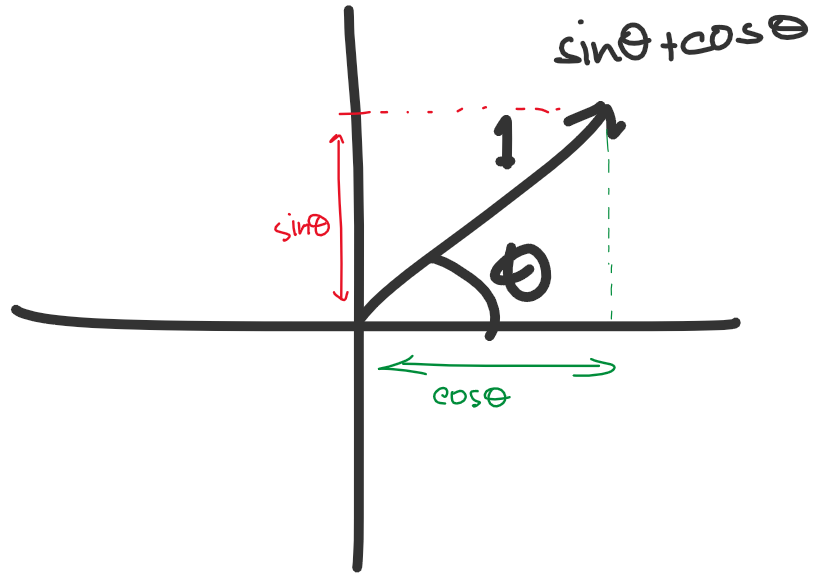
কোড রান করলে ইনফ্লুয়েন্স ভেক্টর ডিকশনারির চেহারা হবে এমন।

{(0, 0): {'angle': 246},
 (0, 8): {'angle': 192},
 ...
 ...
 (8, 16): {'angle': 359},
 (8, 24): {'angle': 234},
 ...
 ...
 (32, 16): {'angle': 305},
 (32, 24): {'angle': 236},
 (32, 32): {'angle': 51}}

ছবিতে দেখতে চাইলে,

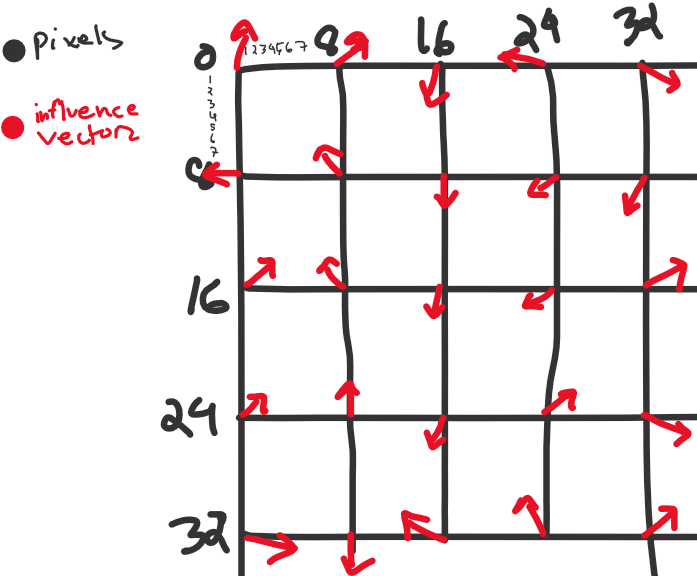
তাহলে প্রতিটা ভেক্টর হবে, \(\hat{i}cos\theta + \hat{j}sin\theta\)। আর যেকোনো পজিশন \((x,y)\) এর জন্য ভেক্টর \(\hat{i}x + \hat{j}y\) এর সাথে ডট প্রোডাক্ট হবে \(xcos\theta + ysin\theta\)

প্রতিটা পিক্সেলের জন্য ডট প্রোডাক্ট সেভ করার জন্য একটা 2D অ্যারে নিই।

arr = np.zeros((SIZE, SIZE))

আমরা এখন প্রতিটা পিক্সেল পজিশনের উপর একটা লুপ চালাবো, (0,0) থেকে (31,31) পর্যন্ত। তবে সরাসরি ০ থেকে ৩১ পর্যন্ত নেস্টেড লুপ না চালিয়ে আমরা প্রতিটা ইনফ্লুয়েন্স ভেক্টরের উপরে লুপ চালাতে পারি। এতে দুইটা সুবিধা হবে, (১) আমরা চার কোণার চারটা ইনফ্লুয়েন্স ভেক্টর সহজে খুঁজে পাবো আর (২) আমাদের lerp এর t-value সহজে ঠিক করতে পারব।

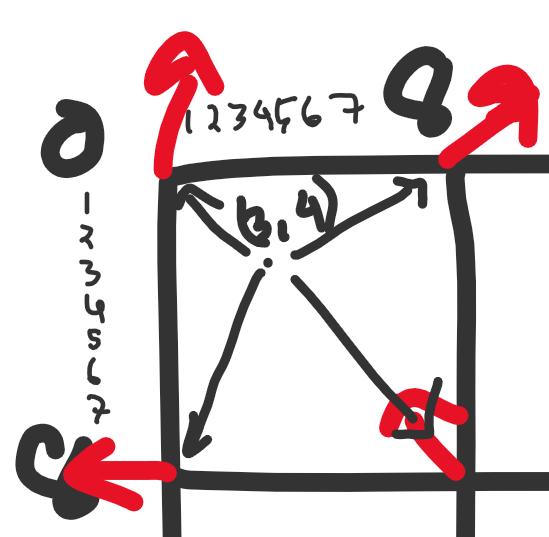
for influence_position in influence_vectors:
    inf_x, inf_y = influence_position

    # যদি আমাদের ইনফ্লুয়েন্স ভেক্টর ইমেজের বাইরে থাকে, তাহলে সেটা পাস করে দিতে হবে। যেমন (০,৩২) পজিশনের ভেক্টরটা
    if inf_x >= SIZE or inf_y >= SIZE: continue

    # এবার চারটা ইনফ্লুয়েন্স ভেক্টরকে ভ্যারিয়েবলের রাখি
    top_left = influence_vectors[(inf_x, inf_y)]
    top_right = influence_vectors[(inf_x+S, inf_y)]
    bottom_left = influence_vectors[(inf_x, inf_y+S)]
    bottom_right = influence_vectors[(inf_x+S, inf_y+S)]

    # ইনফ্লুয়েন্স ভেক্টরটার সেগমেন্টে যতগুলো পিক্সেল আছে তার উপর লুপ চালিয়ে যাই
    for x in range(inf_x, inf_x+S):
        for y in range(inf_y, inf_y+S):
            
            # চারটা ডট প্রোডাক্ট ক্যালকুলেট করি
            dot_tl = get_dot((x,y), (inf_x, inf_y), top_left["angle"])
            dot_tr = get_dot((x,y), (inf_x+S, inf_y), top_right["angle"])
            dot_bl = get_dot((x,y), (inf_x, inf_y+S), bottom_left["angle"])
            dot_br = get_dot((x,y), (inf_x+S, inf_y+S), bottom_right["angle"])

এখানে get_dot আমাদের নিজেদের ডিফাইন করা একটা ফাংশন।

def get_dot(point, influence, angle):
    px, py = point
    ix, iy = influence
    vx, vy = ix-px, iy-py # পিক্সেল থেকে influence vector এর base পর্যন্ত ভেক্টরের x আর y অংশক
    return vx*math.cos(angle) + vy*math.sin(angle)

এবার আমরা উপরের দুইটা ভেক্টরকে একবার আর নিচের দুইটা ভেক্টরকে আরেকবার horizontally lerp করব। এরপর এই দুইটা lerp কে vertically আরেকবার lerp করব।

l1 = lerp(dot_tl, dot_tr, ???)
l2 = lerp(dot_bl, dot_br, ???)
l3 = lerp(l1, l2, ???)

এই ??? এর জায়গায় কি হবে? খেয়াল করে দেখো আমরা কি বলেছিলাম? lerp এর t-value হচ্ছে আমরা দ্বিতীয় ডেটা পয়েন্টের সাথে কতটুকু সাদৃশ্য চাই। আর এই দূরত্ব হতে হবে অবশ্যই সেগমেন্টের সাপেক্ষে, পুরো ইমেজের উচ্চতা বা প্রস্থের সাপেক্ষে না। তাহলে প্রথম পিক্সেলের জন্য t-value হবে 0/8 = 0, পরেরটার জন্য 1/8 = 0.125, পরেরটার জন্য 2/8 = 0.25 এভাবে। একে লেখা যায়,

t_x = x/S - x//S
t_y = y/S - y//S

তাহলে,

arr[x][y] = lerp(
    lerp(dot_tl, dot_tr, t_x),
    lerp(dot_bl, dot_br, t_x),
    t_y
)

# সবশেষে অ্যারের ভ্যালুগুলোকে ০-২৫৫ এই রেঞ্জে স্কেল করলাম কারণ এটা গ্রেস্কেল ইমেজের কালার ভ্যালুর রেঞ্জ
arr = np.interp(arr, (arr.min(), arr.max()), (0, 255))

এবার একে matplotlib এর ইমেজ ভিউয়ারে শো করি।

plt.gray()
plt.imshow(arr)
plt.show()

আউটপুটটা দেখতে কেমন যেন খাপছাড়া লাগছে না? আরেকটু বড় সাইজে দেখি।

SIZE = 128

আমাদের ইমেজটা স্মুথ না। কেন বলতে পারো?

আমাদের t-value টা একটা নির্দিষ্ট পিরিয়ডে লিনিয়ারলি বাড়ছে। আমরা এই ভ্যালুকে একটা Smooth Step ফাংশনে পাস করতে পারি।

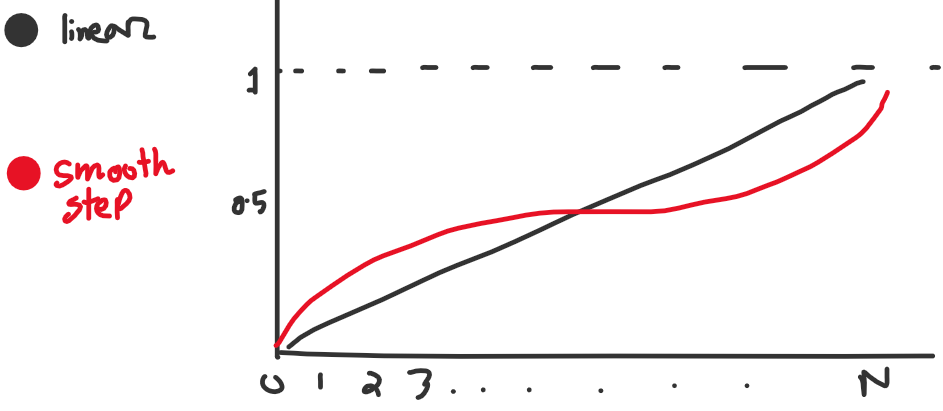
আমি এই Smooth Step ফাংশনটা ইউজ করছি, \(f(x)=6t^5 - 15t^4 + 10t^3\)। তাহলে,

t_x = smooth(x/S - x//S)
t_y = smooth(y/S - y//S)

এইখানে একটা কথা বলে রাখি, তুমি প্রতিবার কোডটা রান করলে ডিফারেন্ট নয়েজ পাবে। কারণ প্রতিবার নতুন নতুন র‍্যান্ডম angle জেনারেট হচ্ছে। এইটা এড়ানোর সহজ উপায় হচ্ছে কোডের শুরুতে একটা seed value সেট করে দেয়া। একটা seed value এর জন্য জেনারেট হওয়া র‍্যান্ডম নাম্বার গুলো সবসময় একই রকম থাকবে।

random.seed(12345)

মনে আছে আমরা প্রতিটা সেগমেন্টে কয়টা পিক্সেল থাকবে (S) সেটা ঠিক করে দিয়েছিলাম? এক কাজ কর, S এর ভ্যালু 64, 32, 16 দিয়ে দেখ আউটপুট কেমন আসে?

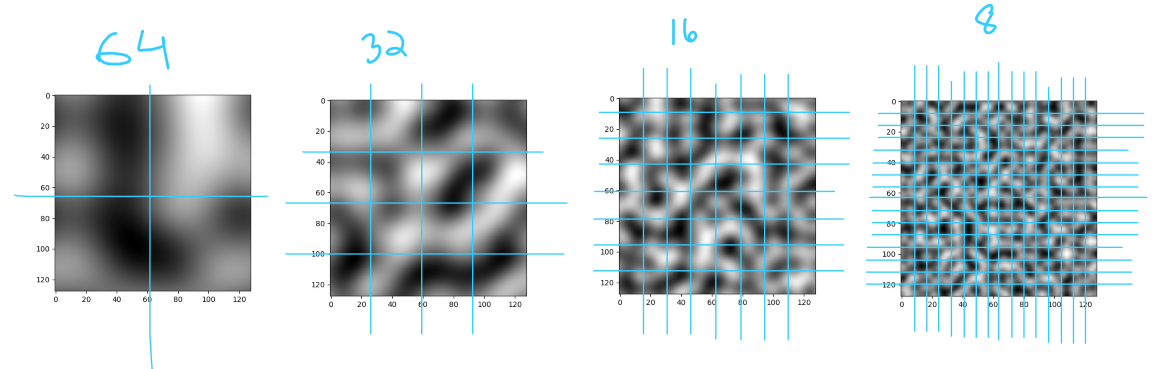
আমরা মূলত ইমেজটাকে horizontally/vertically যথাক্রমে 2, 4, 8 আর 16 ভাগে ভাগ করছি। যত বেশি সেগমেন্ট হচ্ছে আমাদের নয়েজ তত ডিটেইল্ড হচ্ছে। Perlin Noise এর ভাষায় এই ভাগগুলো হচ্ছে Octave আর এগুলোকে 2 এর পাওয়ারে প্রকাশ করা হয়। এখানে আমাদের নয়েজগুলো যথাক্রমে ১, ২, ৩ আর ৪ octave এর। Perlin Noise জেনারেট করার সময় এরকম কয়েকটা অক্টেভের নয়েজ নিয়ে সেগুলোকে overlap করে নতুন নয়েজ বানানো হয়। এই overlapping ও Weighted Average এর মত। কিন্তু এর intesity বা weight কেমন হবে? ধরো, তুমি ফটোশপে (বা অন্য কোনো ইমেজ এডিটরে) একটা ছবির উপর আরেকটা ছবি বসালে। এখন, তোমার পরের ছবির Opacity যদি ১০০% হয়, তাহলে নিচের ছবিটা একেবারেই দেখা যাবে না। তোমার কি করা উচিত? উপরের ছবির Opacity ৫০ তে সেট করলে নিচের ছবিটাও দেখা যাবে, উপরেরটাও দেখা যাবে। এই Opacity টাই আমাদের intesity। Perlin Noise এ একে বলা হচ্ছে Persistence, অর্থাৎ কোনো একটা অক্টেভের নয়েজ কতটুকু persist করছে। একে [0,1] স্কেলে প্রকাশ করা হয়। তোমার persistence যদি 1 বা এর বেশি হয়, তাহলে প্রতিটা অক্টেভের Opacity ১০০% হবে। এর কারণে আগের অক্টেভের কোনো নয়েজ দেখা যাবে না। আবার persistence যদি 0 হয় তাহলে নতুন অক্টেভের কোনো ফিচার পাবো না আমরা। এর মাঝামাঝি কোনো একটা ভ্যালু নিলে আমরা আগের অক্টেভের বৈশিষ্ট্যও রাখতে পারব, সেই সাথে নতুন অক্টেভের কতখানি চাই সেটা ঠিক করে দিতে পারবো। আমরা যদি persistence = 0.5 নিয়ে কাজ করি, তাহলে আমাদের overlapping সিস্টেমটা হবে,

\(1 \times octave_1 + 0.5 \times octave_2 + 0.25 \times octave_3 + \ ...\)

আমরা প্রথমে আমাদের কোডটাকে একটা ফাংশন বানিয়ে ফেলি।

def get_noise(octave, SIZE):
    S = SIZE//int(math.pow(2,octave)) # প্রতিটা সেগমেন্টে কতটা পিক্সেল চাই

    influence_vectors = {} # আমাদের ইনফ্লুয়েন্স ভেক্টরগুলো রাখার জন্য ডিকশনারি

    for i in range(0, SIZE+1, S):
        for j in range(0, SIZE+1, S):
            influence_vectors[(i,j)] = {}
            influence_vectors[(i,j)]["angle"] = random.randint(0,360)

    arr = np.zeros((SIZE, SIZE))

    for influence_position in influence_vectors:
        inf_x, inf_y = influence_position

        # যদি আমাদের ইনফ্লুয়েন্স ভেক্টর ইমেজের বাইরে থাকে, তাহলে সেটা পাস করে দিতে হবে। যেমন (০,৩২) পজিশনের ভেক্টরটা
        if inf_x >= SIZE or inf_y >= SIZE: continue

        # এবার চারটা ইনফ্লুয়েন্স ভেক্টরকে ভ্যারিয়েবলের রাখি
        top_left = influence_vectors[(inf_x, inf_y)]
        top_right = influence_vectors[(inf_x+S, inf_y)]
        bottom_left = influence_vectors[(inf_x, inf_y+S)]
        bottom_right = influence_vectors[(inf_x+S, inf_y+S)]

        # ইনফ্লুয়েন্স ভেক্টরটার সেগমেন্টে যতগুলো পিক্সেল আছে তার উপর লুপ চালিয়ে যাই
        for x in range(inf_x, inf_x+S):
            for y in range(inf_y, inf_y+S):
                t_x = smooth(x/S - x//S)
                t_y = smooth(y/S - y//S)
                
                # চারটা ডট প্রোডাক্ট ক্যালকুলেট করি
                dot_tl = get_dot((x,y), (inf_x, inf_y), top_left["angle"])
                dot_tr = get_dot((x,y), (inf_x+S, inf_y), top_right["angle"])
                dot_bl = get_dot((x,y), (inf_x, inf_y+S), bottom_left["angle"])
                dot_br = get_dot((x,y), (inf_x+S, inf_y+S), bottom_right["angle"])

                arr[x][y] = lerp(
                    lerp(dot_tl, dot_tr, t_x),
                    lerp(dot_bl, dot_br, t_x),
                    t_y
                )
    return arr

তারপর আমরা বিভিন্ন অক্টেভের জন্য শুধু get_noise ফাংশন কল করলেই হবে।

SIZE = 128 # আমাদের ইমেজের দৈর্ঘ্য আর প্রস্থ (পিক্সেলে)

image = 1 * get_noise(2, SIZE) + 0.5 * get_noise(3, SIZE) + 0.25 * get_noise(4, SIZE) + 0.125 * get_noise(5, SIZE)

image = np.interp(image, (image.min(), image.max()), (0, 255))

কোড রান করলে আমার আউটপুট আসে এরকম।

আর এবার যদি বিভিন্ন ব্রাইটনেস রেঞ্জের জন্য বিভিন্ন কালার এসাইন করি,

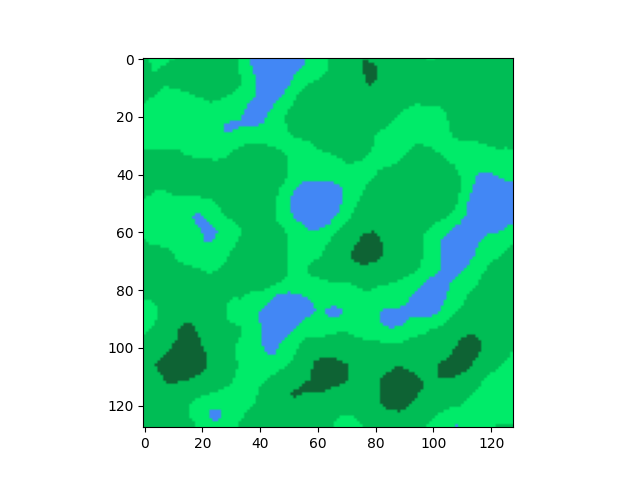
যেমনটা আমরা চেয়েছিলাম।

 

 

Conclusion

উপরের গেমগুলো হয়ত সরাসরি শুধু Perlin Noise ব্যবহার করে না। তবে Noise-বেজড কন্টেন্ট জেনারেশন মেথডগুলোর মোদ্দাকথা মোটামুটি এরকমই। তুমি যখন নিজের গেমের জন্য ম্যাপ জেনারেট করবে, তখন তোমাকে নিজের প্রয়োজনমত এই এলগরিদমে চেঞ্জ আনতে হবে। এছাড়া, আমি 1D/3D Noise নিয়ে কোনো আলোচনা করিনি, কিন্তু তুমি যদি এতক্ষণ পর্যন্ত সবকিছু ঠিকঠাক বুঝে থাকো, তাহলে আশা করছি ওইগুলো বুঝতেও বেশি বেগ পাবে না। আর যদি Noise Generation এর ব্যাপারটা ইন্টারেস্টিং লেগে থাকে, তাহলে এরপর Value Noise, OpenSimplex Noise, Voronoi Noise নিয়ে ঘাঁটাঘাঁটি করতে পারো। নিচের ছবিগুলোর সবকয়টি বিভিন্ন ধরনের নয়েজের মাধ্যমে জেনারেট করা।

তোমার যাত্রা শুভ হোক।

 

 

References

1. Minions (Despicable Me) - Wikipedia
2. • No Man's Sky - Hello Games
   • Spelunky, Nintendo Switch - Nintendo
   • Factorio is going to get a big paid expansion - and not a sequel - Rock Paper Shotgun
   • Survival, Minecraft Wiki - Minecraft Wiki
   • Buy Terraria, Xbox - Xbox
   • RimWorld - Sci-Fi Colony Sim - RimWorld
   • Valheim tips and tricks: a beginner's Valheim guide - Rock Paper Shotgun
   • Civilization V (Video Game) - IMDb
   • Dwarf Fortress on Steam - Steam
3. CS 1003 - Generative Art, Assignment Six - Christopher Andrews
4. Voronoi Noise - Ronja's Tutorials
5. Psychedelic Noise in JRubyArt by monkstone Processing Foundation