On Search Algorithms

2023-04-16

Most people (at least students) learn search algorithms in the context of an academic syllabus, where the material is mostly theoretical. Having taken a course on algorithms as well as teaching others, I have experienced that people find it difficult to properly understand the algorithms without real-world references. This post is an attempt to fill that gap and provide a practical context for search algorithms.

DFS: Solving Sudokus

Sudoku is a popular puzzle game where the objective is to fill a 9x9 grid with digits so that each column, each row, and each of the nine 3x3 sub-grids that compose the grid contains all of the digits from 1 to 9. The puzzle setter provides a partially filled grid, which for a well-posed puzzle has a single solution. (Source: Wikipedia)

Depth-first search starts at the root (or some arbitrary starting node) of a tree/graph data structure and explores as deep as possible along each branch before backtracking. Wikipedia provides a very nice example of DFS on a tree:

Solving a sudoku puzzle in this technique will be something like this:

Fill in the first empty cell validly. If you cannot, undo the previous change and try the next valid number.
If the puzzle is solved, nice!
If not, go to step 1.

Once again, Wikipedia has us covered:

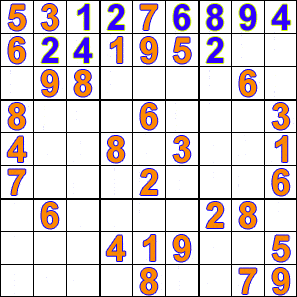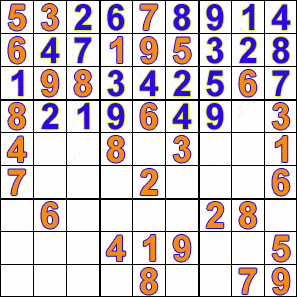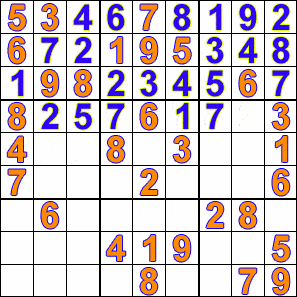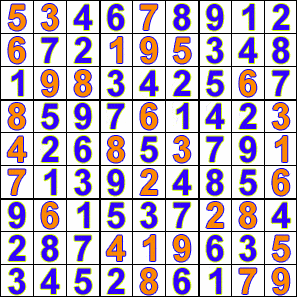
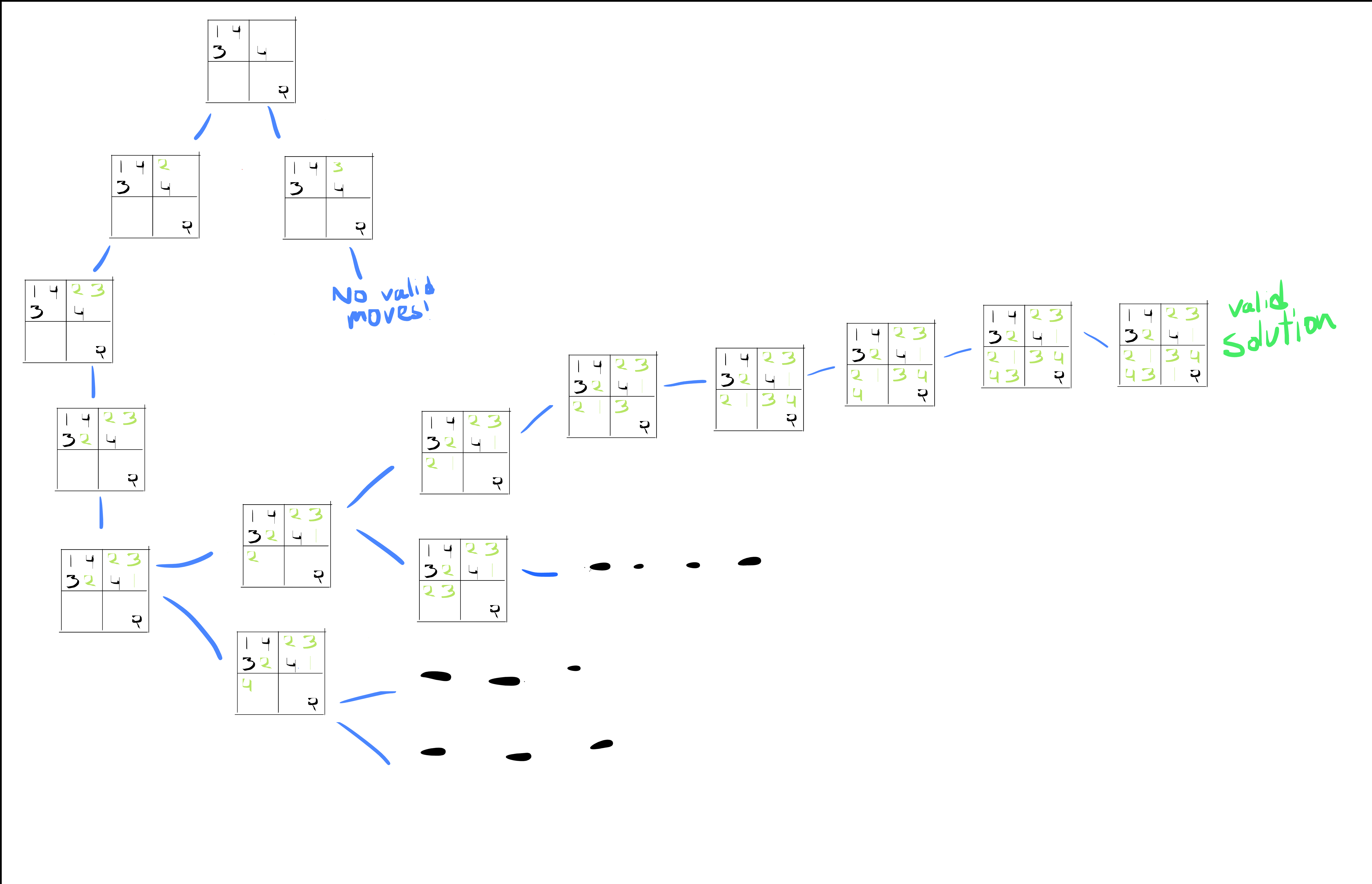
So, what does the search tree look like?

For the sake of explanation, let us dumb down problem. Consider a 4x4 grid, subdivided into four 2x2 squares. The objective is to fill the grid with digits so that each row, each column, and each of the four 2x2 sub-grids contains all of the digits from 1 to 4.

Suppose the partially filled grid is this:

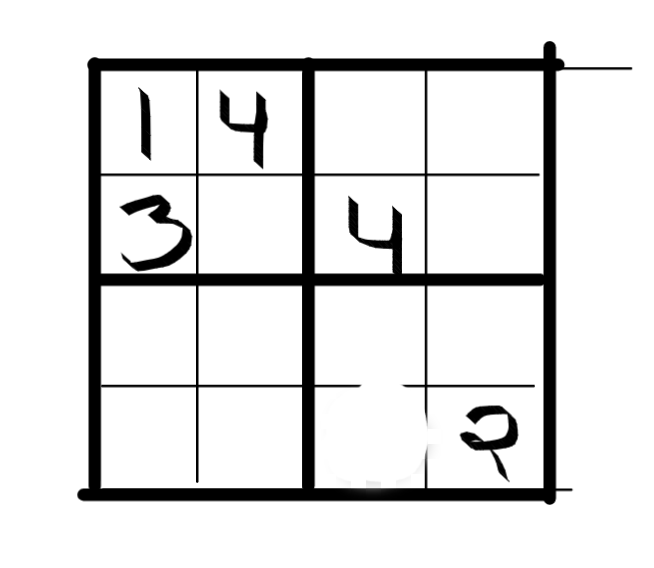
The search tree will look like this:

First, let's define the Sudoku board as a 2D array.

sudoku = [
    [0, 5, 0, 1, 0, 8, 9, 0, 0],
    [0, 0, 0, 0, 7, 6, 0, 2, 1],
    [7, 0, 0, 3, 0, 0, 4, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 2],
    [0, 3, 9, 0, 0, 0, 0, 5, 0],
    [0, 1, 0, 0, 9, 0, 0, 0, 0],
    [0, 0, 5, 0, 0, 9, 0, 0, 7],
    [0, 0, 0, 2, 0, 3, 0, 0, 0],
    [0, 0, 0, 4, 0, 7, 0, 0, 0]
]

Following the steps above, define a function to find the first empty cell in the board.

def find_first_empty(s):
    for i in range(len(s)):
        for j in range(len(s[0])):
            if s[i][j] == 0:
                return (i, j)
    return None

Now, what is a valid move? Given the board, a digit, and a position on the board (a row-column tuple), we can check if the board is free of inconsistencies if we place the digit at that position. We can do this by checking if the digit is present in the row, column, and the 3x3 sub-grid, and if the position is empty.

def is_valid(s, num, pos):
    # Check row
    for i in range(len(s[0])):
        if s[pos[0]][i] == num and pos[1] != i:
            return False

    # Check column
    for i in range(len(s)):
        if s[i][pos[1]] == num and pos[0] != i:
            return False

    # Check box
    box_x = pos[1] // 3
    box_y = pos[0] // 3

    for i in range(box_y * 3, box_y * 3 + 3):
        for j in range(box_x * 3, box_x * 3 + 3):
            if s[i][j] == num and (i, j) != pos:
                return False

    return True

We have everything we need for implementing our solution. Let's define a solver function.

def solve(board):

    # Our code here

First, find the first empty cell.

empty_pos = find_first_empty(board)

If there is no empty position, that means the sudoku is solved. We can return the board as it is. This serves as the base case for our recursive function.

if not empty_pos:
        print_sudoku(board)
        return True

Otherwise, we loop through the numbers 1 to 9 and check if is_valid(board, digit, position) returns a True value. If it does, place the digit in that position. Then, recursively call the solve function. If the recursive call returns True, we can return True from the current call. If not, we can backtrack and try the next digit.

else:
    row, col = empty_pos
    for i in range(1,10):
        if is_valid(s, i, (row, col)):
            s[row][col] = i
            if solve(s):
                return True
            s[row][col] = 0
    return False

Notice the line s[row][col] = 0. This is important. We need to do this because, in python, everything between functions is passed by reference, unless mentioned otherwise explicitly. If we don't reset the value of the cell to 0, we will end up with an incorrect solution.

Running the solver on our board outputs this,

0 5 0 | 1 0 8 | 9 0 0
0 0 0 | 0 7 6 | 0 2 1
7 0 0 | 3 0 0 | 4 0 0
---------------------
0 0 0 | 0 0 0 | 0 0 2
0 3 9 | 0 0 0 | 0 5 0
0 1 0 | 0 9 0 | 0 0 0
---------------------
0 0 5 | 0 0 9 | 0 0 7
0 0 0 | 2 0 3 | 0 0 0
0 0 0 | 4 0 7 | 0 0 0

SOLUTION:

2 5 6 | 1 4 8 | 9 7 3
3 4 8 | 9 7 6 | 5 2 1
7 9 1 | 3 2 5 | 4 6 8
---------------------
4 6 7 | 5 3 1 | 8 9 2
8 3 9 | 7 6 2 | 1 5 4
5 1 2 | 8 9 4 | 7 3 6
---------------------
1 2 5 | 6 8 9 | 3 4 7
9 7 4 | 2 1 3 | 6 8 5
6 8 3 | 4 5 7 | 2 1 9

which is correct.

Notice how everything fell in place after we were able to express the problem using a graph (or tree, in this case). A wide variety problems can be put under graph theory with a good eye for abstraction. Our first takeway from this post is that, try to express your problem as a graph, tree or network. Once that is possible, it will be trivial to use graph algorithms on the problemm.